NOMBRES COMPREXES
Télécharger le fichier cplx03.pdf
Nombres complexes
Les nombres complexes prolongent l'ensemble des nombres réels. Se composant d'une partie réelle et d'une partie imaginaire, ils se représentent par un point à deux coordonnées dans le plan, que l'on appelle alors plan complexe. Ils permettent, par exemple, de donner des solutions à l'équation 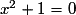 .
.
Les nombres complexes permettent de caractériser facilement les transformations du plan, en particulier la rotation qui peut être définie par une simple multiplication.
Leurs applications sont nombreuses en électromagnétisme et en électronique, car leur écriture trigonométrique permet de simplifier la transcription des phénomènes ondulatoires.
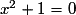 .
.Les nombres complexes permettent de caractériser facilement les transformations du plan, en particulier la rotation qui peut être définie par une simple multiplication.
Leurs applications sont nombreuses en électromagnétisme et en électronique, car leur écriture trigonométrique permet de simplifier la transcription des phénomènes ondulatoires.
1. Quelles sont les différentes écritures d'un nombre complexe ?
Un nombre complexe z a une écriture algébrique de la forme :
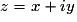 (x
(x 
 ; y
; y 
 ; i2 = −1).
; i2 = −1).
Le premier terme constitue sa partie réelle et le second sa partie imaginaire.
On note : Re(z) = x et Im(z) = y.
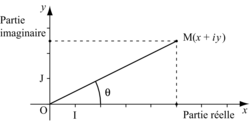
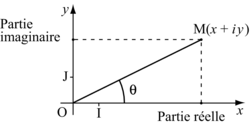
Dans le repère orthonormal direct (O ; I, J), z se représente par le point M(x ; y).
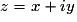 (x
(x 
 ; y
; y 
 ; i2 = −1).
; i2 = −1).Le premier terme constitue sa partie réelle et le second sa partie imaginaire.
On note : Re(z) = x et Im(z) = y.
Dans le repère orthonormal direct (O ; I, J), z se représente par le point M(x ; y).
On dit que le point M et le vecteur 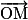 ont pour affixe z.
ont pour affixe z.
Le module r du nombre complexe z est la longueur OM :
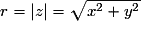 .
.
L'argument du nombre complexe non nul z est l'angle orienté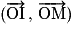 .
.
On note :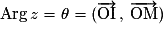 .
.
z peut alors s'écrire sous forme trigonométrique :
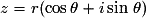 .
.
Sous forme exponentielle :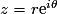 .
.
Exercice n°1Exercice n°2
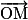 ont pour affixe z.
ont pour affixe z.Le module r du nombre complexe z est la longueur OM :
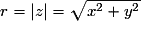 .
.L'argument du nombre complexe non nul z est l'angle orienté
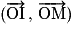 .
.On note :
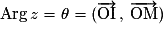 .
.z peut alors s'écrire sous forme trigonométrique :
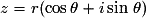 .
.Sous forme exponentielle :
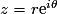 .
.Exercice n°1Exercice n°2
2. Qu'est-ce qu'un nombre complexe conjugué ?
Le nombre complexe conjugué de 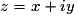 est le complexe
est le complexe 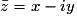 .
.
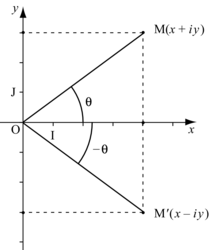
Dans le plan complexe, si le point M a pour affixe z et M' pour affixe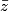 , alors M et M' sont symétriques par rapport à l'axe des abscisses.
, alors M et M' sont symétriques par rapport à l'axe des abscisses.
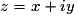 est le complexe
est le complexe 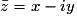 .
.Dans le plan complexe, si le point M a pour affixe z et M' pour affixe
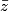 , alors M et M' sont symétriques par rapport à l'axe des abscisses.
, alors M et M' sont symétriques par rapport à l'axe des abscisses.Le produit d'un nombre complexe par son conjugué est un nombre réel égal au carré de leur module commun :
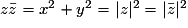 .
.
Le conjugué de la somme est égal à la somme des conjugués :
si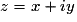 et
et 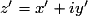 , alors :
, alors :
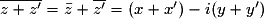 .
.
Le conjugué du produit est égal au produit des conjugués :
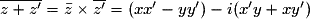 .
.
Exercice n°3Exercice n°4
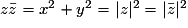 .
.Le conjugué de la somme est égal à la somme des conjugués :
si
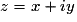 et
et 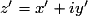 , alors :
, alors :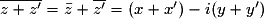 .
.Le conjugué du produit est égal au produit des conjugués :
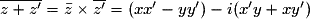 .
.Exercice n°3Exercice n°4
3. Comment résoudre une équation du second degré à coefficients réels dans l'ensemble des nombres complexes ?
Considérons l'équation du second degré à coefficients réels :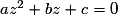 (a
(a 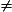 0).
0).Sur l'ensemble des nombres réels, l'existence de solutions dépend du signe du déterminant
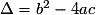 .
.
- si Δ
 0, il y a deux solutions :
0, il y a deux solutions : 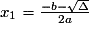 et
et 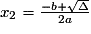 ;
; - si Δ < 0, il n'y a pas de solution.
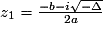 et
et 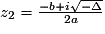 .
.Exercice n°5
4. Quelles sont les propriétés des nombres complexes ?
Soient deux nombres complexes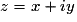 et
et 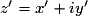 (x
(x 
 ; y
; y 
 ; x'
; x' 
 ; y'
; y' 
 ).
).• Égalité
Deux nombres complexes sont égaux si et seulement si leurs parties entières sont égales ainsi que leurs parties imaginaires :
z = z' si et seulement si x = x' et y = y'.
Deux nombres complexes sont égaux si et seulement si leurs parties entières sont égales ainsi que leurs parties imaginaires :
z = z' si et seulement si x = x' et y = y'.
• Somme
La partie réelle du complexe somme est la somme des parties réelles, et la partie imaginaire est la somme des parties imaginaires :
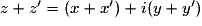 .
.
La partie réelle du complexe somme est la somme des parties réelles, et la partie imaginaire est la somme des parties imaginaires :
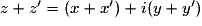 .
.• Produit
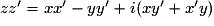
Le module du complexe produit est le produit des modules :
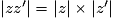 .
.
L'argument du complexe produit est la somme des arguments :
arg(z × z') = arg z + arg z'.
Soit pour la forme trigonométrique :
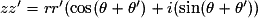 .
.
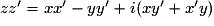
Le module du complexe produit est le produit des modules :
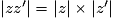 .
.L'argument du complexe produit est la somme des arguments :
arg(z × z') = arg z + arg z'.
Soit pour la forme trigonométrique :
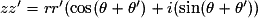 .
.• Quotient
Pour obtenir l'écriture algébrique du complexe quotient on multiplie numérateur et dénominateur par le complexe conjugué du dénominateur.
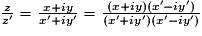 . Soit :
. Soit : 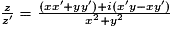 .
.
Le module du quotient est le quotient des modules :
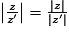 .
.
L'argument du quotient est la différence des arguments :
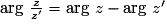 (z
(z 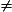 0 et z'
0 et z' 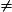 0) .
0) .
Soit pour la forme trigonométrique :
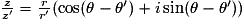 .
.
Exercice n°6Exercice n°7
Pour obtenir l'écriture algébrique du complexe quotient on multiplie numérateur et dénominateur par le complexe conjugué du dénominateur.
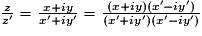 . Soit :
. Soit : 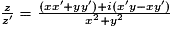 .
.Le module du quotient est le quotient des modules :
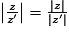 .
.L'argument du quotient est la différence des arguments :
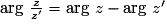 (z
(z 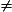 0 et z'
0 et z' 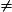 0) .
0) .Soit pour la forme trigonométrique :
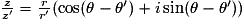 .
.Exercice n°6Exercice n°7
5. Quelles sont les écritures complexes des transformations ?
Par une transformation, un point M d'affixe z a pour image le point M' d'affixe z'.Si la transformation est une translation de vecteur
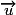 d'affixe a, alors :
d'affixe a, alors : 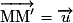 et
et 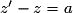 .
.D'où :
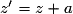 .
.Si la transformation est une homothétie de centre Ω d'affixe ω et de rapport k, alors
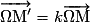 et
et 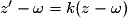 .
.Si la transformation est une rotation de centre O et d'angle θ, alors :
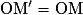 et
et 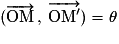 .
.En posant
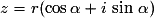 ,
,alors :
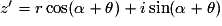 ,
,soit :
![z^{\prime}=r[(\cos\alpha\cos\theta-\sin\,\alpha\sin\theta)+i(\sin\,\alpha\,\cos\theta+\sin\,\theta\cos\alpha)]](http://static1.assistancescolaire.com/t/images/tsti_mat_06_m53.png)
En remarquant que :
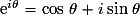 , on a alors :
, on a alors : 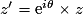 .
.Si la transformation est une rotation de centre Ω d'affixe ω et d'angle θ, alors
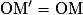 et
et 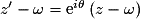 .
.Exercice n°8Exercice n°9
À retenir
Un nombre complexe z a une écriture algébrique de la forme :
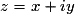 (x
(x 
 ; y
; y 
 ; i2 = −1).
; i2 = −1).
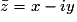 est le complexe conjugué de z.
est le complexe conjugué de z.
Dans le repère orthonormal direct (O ; I, J),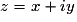 se représente par le point M(x ; y). On dit que M et
se représente par le point M(x ; y). On dit que M et 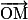 ont pour affixe z.
ont pour affixe z.
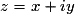 (x
(x 
 ; y
; y 
 ; i2 = −1).
; i2 = −1).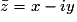 est le complexe conjugué de z.
est le complexe conjugué de z.Dans le repère orthonormal direct (O ; I, J),
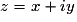 se représente par le point M(x ; y). On dit que M et
se représente par le point M(x ; y). On dit que M et 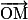 ont pour affixe z.
ont pour affixe z.Module : 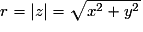 .
.
Argument : 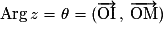 .
.
Écriture trigonométrique : 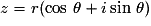 .
.
Écriture exponentielle : 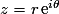
Translation de vecteur 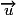 d'affixe a, M(z)
d'affixe a, M(z)  M'(z') :
M'(z') : 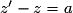 .
.
Homothétie de centre Ω d'affixe ω et de rapport k :
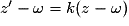 .
.
Rotation de centre O et d'angle θ : 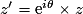 .
.
Rotation de centre Ω d'affixe ω et d'angle θ : 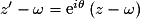 .Télécharger le fichier tscompcours.pdf
.Télécharger le fichier tscompcours.pdf